A2L Item 026
- Description: Order the extent of compression of an internal spring in a 2 mass system given the same total force and mass.
- Goal: Reasoning with 2nd law.
- Source: UMPERG
- Keywords: Forces, Mechanics, Reasoning, Dynamics, Springs
The question for students:
Consider the three situations shown below. In each case two small carts are connected by a spring. A constant force F is applied to the leftmost cart in each case. In each situation the springs are compressed so that the distance between the two carts never changes.
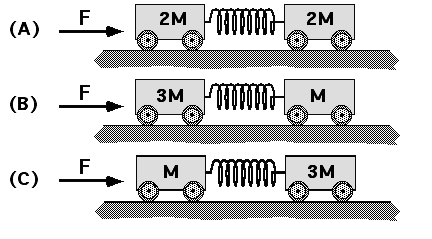
Which of the following statements must be true regarding the compression of the spring in each case? Assume the springs are identical.
- Compression A = Compression B = Compression C
- B = C < A
- A < B = C
- A < B < C
- B < A < C
- C < A < B
- A < C < B
- None of the above
- Cannot be determined
Commentary for teachers:
Answer
(5) The total mass is the same so the acceleration of the systems must be the same. In each case the spring exerts the only horizontal force on the cart to the right. The spring force must be largest for the 3M cart and smallest for the M cart: B < A < C.
Background
This item requires students to reason. It is difficult to resort to equation manipulation to answer this question. One difficulty with the problem is that it involves a complex system (two carts connected by a spring).
Questions to Reveal Student Reasoning
Is it really possible to compress the carts so that they stay a fixed distance apart? What forces act on each cart? Will the carts accelerate or move with a constant velocity? Compare the carts acceleration.
Suggestions
Draw a free-body diagram for each cart.
Define a new problem in terms of the carts on the right: Each cart is given an applied force so that each has the same acceleration. How do the applied forces compare?